Korrelationen und wie du davon profitierst
Veröffentlicht am 17.07.2023 | Lesedauer: 15 Minuten
Von Jan Fuhrmann
▲ Korrelationen | Risikomanagement und Marktverständnis
Die meisten Trader und Investoren untersuchen Einzelwerte immer einzeln, aber letzten Endes ist der gesamte Markt ein großes ganzes Gebilde. Aus diesem Grund korrelieren einige Basiswerte stark miteinander und andere verlaufen sogar entgegengesetzt, was man im aktiven Handel unbedingt berücksichtigen sollte. Diese Korrelationen sind messbar und als Trader und Investor kann man im Handel davon profitieren. In diesem Blog geht es einerseits um die Theorie, aber auch um die wichtigsten Korrelationen am Markt, die man bei jeder Analyse und beim Trading berücksichtigen sollte.
Basics
Was sind Korrelationen?
Wenn sich zwei Aktien ähnlich entwickeln, dann sagt man auch: Sie korrelieren miteinander. Dies gilt natürlich nicht nur für Aktien, sondern für Rohstoffe, Indizes, Forex, … gleichermaßen. Die Korrelation kann dabei verschiedene Ausmaße annehmen und entweder sehr stark ausgeprägt sein (Gleichlauf bei einer perfekten positiven Korrelation), eher schwach oder sogar negativ sein. Bei einer perfekten negativen Korrelation entwickeln sich die betrachteten Basiswerte genau gegenläufig, also entgegengesetzt zueinander – ein sehr spannendes Szenario, wenn es um das Thema Risikomanagement und die Vermeidung von größeren Verlusten als Anleger oder Trader geht. Beim Management eines Depots kann mit der Kenntnis über die Korrelationen das Gesamtrisiko mit einem diversifizierten Depotaufbau reduziert werden. Es ist jedoch ein Mythos, dass man einfach nur viele verschiedene Werte kaufen muss – dadurch kann man sein Depot nicht gezielt diversifizieren (bzw. es wäre ineffizient und nicht zielführend). Um das Gesamtrisiko wirklich zu senken, bedarf es zwangsläufig der Berücksichtigung aller Korrelationen der Einzelwerte.
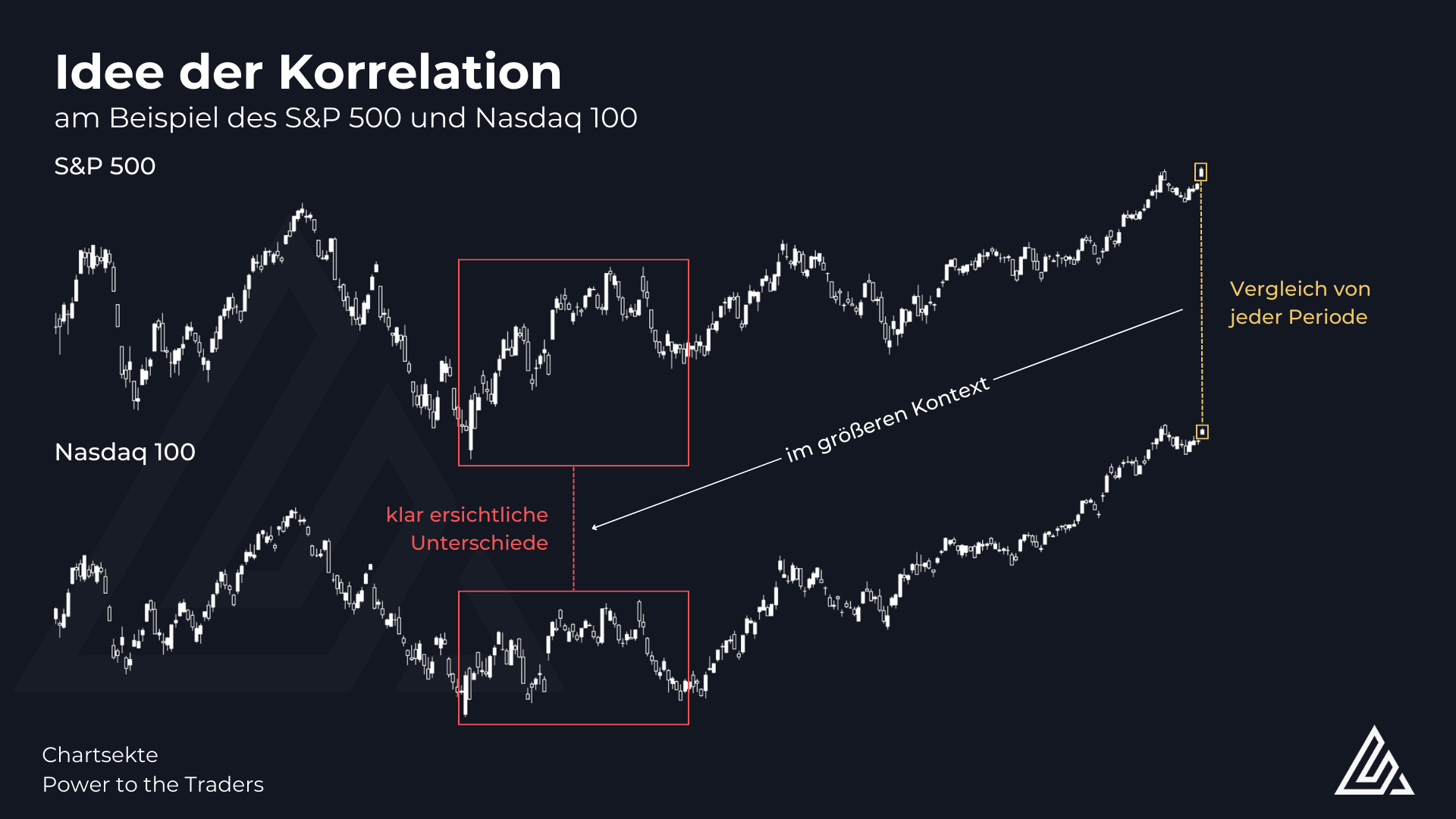
Ein sehr simples Beispiel für eine starke Korrelation zeigt eine Analyse vom S&P 500 und Nasdaq 100. Es ist aufgrund der enthaltenen Aktien wenig überraschend, dass beide Indizes sich grundsätzlich ähnlich entwickeln, aber natürlich ist diese Korrelation mal stärker und mal schwächer. In der nachfolgenden Abbildung ist das gut erkennbar: Betrachtet man nur den letzten Handelstag, dann ist eine große Ähnlichkeit auffällig. Blickt man jedoch auf das große Ganze, dann gibt es im größeren Zeitrahmen auch Phasen, in denen die Entwicklung der beiden Aktienindizes voneinander abweichen.
Wie werden Korrelationen berechnet?/Wie misst man Korrelationen?
Dass bspw. beim Nasdaq 100 und S&P 500 ein Zusammenhang in der Entwicklung besteht, ist sofort klar – das sieht man in der Abbildung sowohl während der Aufwärtsphasen, aber auch wenn ein Abwärtstrend aktiv war. Um das nun aber auch für sich nutzen zu können, sollte man die Stärke dieser Korrelation im Detail messen können. Es wird nun etwas mathematisch, aber ich versuche das Prinzip dahinter möglichst simpel auch in einfache Worte zu fassen.
Korrelationskoeffizient
Der Korrelationskoeffizient ist der gängige Maßstab um die Stärke einer Korrelation in einem bestimmten Zeitrahmen zu messen. Er kann Werte von -1 bis 1 annehmen, wobei -1 einer perfekten negativen Korrelation entspricht (die beiden Basiswerte entwickeln sich also genau entgegengesetzt) und 1 einer perfekten positiven Korrelation (die beiden Basiswerte entwickeln sich also immer in eine Richtung/im Gleichlauf).
Bei der Berechnung muss zunächst festgelegt werden über welchen Zeitraum und in welcher Zeiteinheit eine Korrelation untersucht werden soll. Wir nehmen nun beispielhaft immer den Tages-Chart (also die Tages-Renditen) und einen betrachteten Zeitraum von 100 Tagen. Im Folgenden eine Erklärung zur Berechnung – wem das zu viel ist, der überspringt die kursiven Absätze.
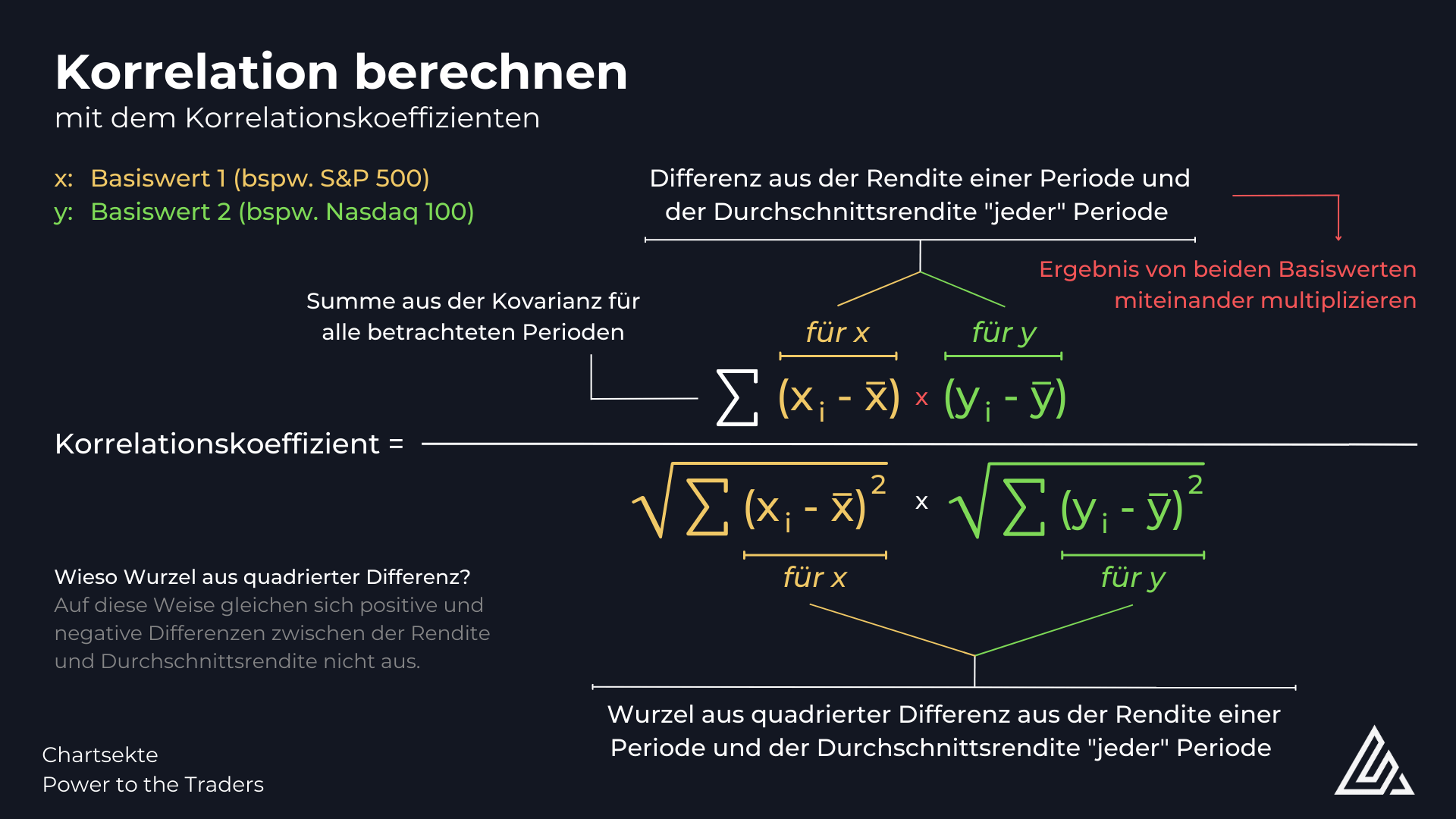
Da wir wissen möchten wie wahrscheinlich es ist, dass sich beide Basiswerte in dieselbe Richtung bewegen, untersuchen wir nun jeden Tag einzeln. Dabei ermitteln wir jeweils die Differenz aus der Tagesrendite und der durchschnittlichen Tagesrendite (in diesen 100 Tagen) und multiplizieren die Ergebnisse für beide Basiswerte miteinander. Das wird für jeden Tag in der gesamten Laufzeit wiederholt und die Ergebnisse addiert.
>> Aber warum? Die Antwort ist ziemlich einfach. Für ein sehr vereinfachtes Beispiel (es geht hier nur ums Prinzip) nehmen wir mal an die Durchschnittsrendite beider Basiswerte belief sich auf 0, sodass wir nur noch die Tagesrenditen betrachten müssen. Sind beide Tagesrenditen positiv, ergibt sich bei der Multiplikation ein positiver Wert. Sind beide Tagesrenditen negativ, ergibt sich wieder ein positiver Wert. Nur wenn die Entwicklung beider Basiswerte unterschiedlich war, ergibt sich ein negativer Wert. Macht man das nun für jeden Tag, dann wird die Gesamtsumme von dieser Rechnung umso größer, wenn sich beide Basiswerte in eine Richtung entwickeln. Entwickeln sie sich entgegengesetzt, dann wird die Gesamtsumme umso kleiner bzw. sogar negativ. Wir können an der Stelle also schon einmal klar unterscheiden ob die beiden Basiswerte sich eine eine tendenziell in Richtung bewegen oder nicht.
Mit diesem ersten Teil der Berechnung haben wir nun schon einmal eine Tendenz, aber wirklich vergleichbar ist das Ergebnis nicht. Betrachtet man bspw. die Korrelation für 10 Tage, dann ist die Summe natürlich viel kleiner als für 1.000 Tage. Es bedarf also noch einem geeigneten Nenner, der aus diesem Zwischenergebnis einen wirklichen vergleichbaren Koeffizienten macht.
Wem das Prinzip der Standardabweichung geläufig ist, der erkennt sofort was in der Formel unter dem Bruchstrich steht. Hier wird wieder jede Differenz aus der Tagesrendite und der durchschnittlichen Tagesrendite gebildet. Auf diese Weise wird wieder die Abweichung (entweder positiv oder negativ, also höhere oder niedrigere Rendite als im Durchschnitt) errechnet. Statt dies aber nun von beiden Basiswerten miteinander multiplizieren, multipliziert man den Wert mit sich selbst. Das führt dazu, dass wir hinterher bei der Summenbildung nicht das Problem haben, dass sich positive und negative Abweichungen vom Durchschnitt einfach ausgleichen. Weicht ein Basiswert schließlich einmal um 3 % und einmal um -3 % vom Durchschnittswert ab, dann sollen diese beiden Abweichungen ja nicht einfach ignoriert werden (sonst würde man das ja so behandeln als ob es nie eine Abweichung gegeben hätte). Das ist das typische Prinzip der Varianzermittlung. Auch hier wird im Anschluss wieder die Summe für alle quadrierten Abweichungen gebildet, also letztendlich so wie im ersten Teil der Gesamtrechnung. Diesen Schritt macht man für beide Basiswerte, multipliziert das Ergebnis und zieht am Ende die Wurzel.
>> Warum das Ganze? Es klingt komplizierter als es ist. Wir machen im gesamten “unteren Teil” der Rechnung genau dasselbe wie im “oberen Teil”. Wir betrachten dieses Mal aber jeden Basiswert einzeln und gucken uns nicht den Zusammenhang beider Renditen an (also ob die beide positiv, beide negativ oder verschieden sind), sondern einfach nur die Abweichungen. Da wir dieselben Werte wie in der ersten Teilrechnung verwenden, haben wir auf diese Weise einen Teiler in der perfekten Größe um einen Koeffizienten zu errechnen.
Das Prinzip ist schriftlich nicht so leicht zu erklären, aber zumindest der Grundgedanke sollte verständlich sein: Einmal schauen wir uns an ob die Renditen beider Basiswerte in dieselbe Richtung abweichen oder sich entgegengesetzt entwickeln – dieser obere Part der Berechnung bestimmt darüber ob die Korrelation positiv oder negativ ist. Danach ermitteln wir einen geeigneten Teiler, der das Ganze noch um die allgemeine Volatilität bereinigt.
In der Praxis
Kein Mensch setzt sich nun hin und rechnet jeden Tag den Korrelationskoeffizienten für die Bewegungen von zwei Anlagen neu aus – das ist viel zu zeitraubend. Bei TradingView gibt es allerdings einen Indikator, welcher “Correlation & Beta” heißt. Öffnet man einen Chart, dann kann man bei dem Indikator den zweiten Basiswert eingeben, zu dem die Korrelation bestimmt werden soll. Auch die Einstellung der Zeitperiode ist möglich, für die man die Korrelation der Anlagen überprüfen möchte.
Beta-Faktor
Bei dem genannten Tool gibt es zusätzlich den Beta-Faktor. Dieser hängt mit dem Korrelationskoeffizienten unmittelbar zusammen, aber enthält zugleich auch Informationen über die Volatilität eines Werts. Aus diesem Grund ist er nicht auf eine Wertspanne zwischen -1 und 1 begrenzt, sondern kann auch Werte jenseits davon annehmen. Ein Beta-Faktor von 2 zeigt bspw. eine starke Korrelation an und zugleich eine doppelt so hohe Volatilität. Steigt der Vergleichswert also um 1 %, dann steigt der andere Wert um 2 %. In der Regel wird dies in Bezug zum Gesamtmarkt verwendet.
Warum sollte man auf Korrelationen achten?
Korrelationen sind in mehrerer Hinsicht nützlich in der Praxis und von hoher Bedeutung. Der erste und gleichzeitig offensichtlichste Punkt ist das Risiko-Management, was sowohl für ein langfristiges Portfolio als auch für Trades gilt. Viele achten darauf, dass ein einzelner Trade kein zu hohes Risiko für das Gesamtdepot darstellt und wählen ihre Positionsgröße entsprechend? Aber was ist, wenn man mehrere Trades offen hat, bei denen die Basiswerte nahezu perfekt korrelieren? Dieser Punkt wird häufig vergessen, aber dem Risiko sollte man sich in der Praxis bewusst sein. Offensichtlich ist das im Forex-Bereich, wo bspw. alle JPY-Paare natürlich bis zu einem gewissen Grad miteinander korrelieren. Im letzten Monat hatten der GBPJPY und EURJPY bspw. eine Korrelation in Höhe von 95,70 %. Handelt man beide Long, dann ist es schon fast so, als ob man einen Trade mit doppeltem Risiko nimmt.
Korrelationen sind allerdings auch beim Entdecken von Trade-Ideen von hilfreicher Bedeutung. Wie wir später noch sehen werden haben bspw. Gold und Silber eine recht hohe Korrelation. Ist bspw. Gold bereits der Ausbruch aus einer Bodenbildung gelungen und ein Einstieg zu spät, dann bietet sich bei Silber ggf. noch eine Chance.
Korrelationen von Währungspaaren / Währungskorrelationen
Am Gesamtmarkt kann man grundsätzlich den Korrelationskoeffizienten von dem Kurs von jedem Wertpapier mit einem anderen Wertpapier berechnen (egal um welche Anlageklasse es geht: Anleihen, Aktien, Rohstoffe, Forex bzw. Währungen, …). Im nächsten Abschnitt dieses Blogs werden wir auch genau das tun und verschiedenste Märkte und Anlageklassen und deren Beziehung zueinander betrachten. Nun soll es aber erst einmal um den Devisenmarkt und somit um Währungskorrelationen gehen, denn der Forex Markt ist besonders bekannt für auffällige Beziehungen. Speziell im Trading sollte der Zusammenhang unterschiedlicher Währungen berücksichtigt werden, damit man nicht unbewusst mehrere Trades eröffnet, die stark korreliert sind. Geht einer nicht auf, dann fallen die Verluste im Portfolio von dem Anleger unter Umständen wesentlich höher aus als eingeplant.
Es gibt einige Währungspaare am Forex Markt (Devisenmarkt), die dafür bekannt sind, dass sie stark miteinander korreliert sind. Bspw. ist die Beziehung zwischen dem AUD / USD (AUD = Australischer Dollar und USD = US Dollar) und dem NZD / USD (Neuseeländischer Dollar zum US Dollar) im letzten Jahr mit einem Korrelationskoeffizienten von 0,90 als extrem hoch einzuordnen. Das ist allerdings kein einzigartiger Fall. Ähnlich stark (0,96) ist die Wechselbeziehung im Fall vom USD / JPY und dem CAD / JPY. Natürlich überraschen solche Korrelationen nur teilweise, denn eine Währung bei beiden Währungspaaren ist immer dieselbe. Nichtsdestotrotz liegt es noch immer an der anderen Währung wie hoch die Wechselbeziehung zwischen beiden Währungspaaren ist. Im selben Zeitrahmen kann vom GBP / JPY (GBP = Britisches Pfund und JPY = Japanischer Yen) zum USD / JPY bspw. keine so starke Währungskorrelation festgestellt werden. Nur weil eine Währung des Paars also gleich ist, müssen die Kursentwicklungen und Bewegungen beider Paare nicht stark korrelierend sein.
Was sind die wichtigsten Korrelationen am Markt? – Exklusiv für Chartsekten Mitglieder
Bitte logge dich ein, um diesen Teil zu lesen
Jan Fuhrmann
Transparenzhinweis und Haftungsausschluss:
Die Autoren haben diesen Beitrag nach bestem Wissen und Gewissen erstellt, können die Richtigkeit der angegebenen Informationen und Daten aber nicht garantieren. Es findet keinerlei Anlageberatung durch „Chartsekte“, oder durch einen für „Chartsekte“ tätigen Autor statt. Dieser Beitrag soll eine journalistische Publikation darstellen und dient ausschließlich Informationszwecken. Die Informationen stellen keine Aufforderung zum Kauf oder Verkauf von Wertpapieren dar. Börsengeschäfte sind mit erheblichen Risiken verbunden. Wer an den Finanz- und Rohstoffmärkten handelt, muss sich zunächst selbstständig mit den Risiken vertraut machen. Der Kunde handelt immer auf eigenes Risiko und eigene Gefahr. „Chartsekte“ und die für uns tätigen Autoren übernehmen keine Verantwortung für jegliche Konsequenzen und Verluste, die durch Verwendung unserer Informationen entstehen. Es kann zu Interessenkonflikten kommen, durch Käufe und einen darauffolgenden Profit durch eine positive Kursentwicklung von in Artikeln erwähnten Aktien oder anderen Werten.
Mehr Infos unter: https://chartsekte.de/haftungsausschluss/